Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Файлы
• Литература

Заблоцкий В.Р. 1 Кириченко А.С. 1

---

1 Московский государственный университет геодезии и картографии

Статья в формате PDF

0 KB

1. Заблоцкий В.Р. Особенности преподавания информатики в вузе геодезического профиля на современном этапе. // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2015. – № 6. – С. 119–125.

2. Заблоцкий В.Р., Клыпин И.А. Опыт использования программы удаленного администрирования в учебном процессе МИИГАиК. Сборник статей по итогам научно-технических конференций, посвященных 235-летию основания МИИГАиК, выпуск 7, ч. 2. – М.: МИИГАиК. – 2014. – С. 106–109.

3. Заблоцкий В.Р. Обучение языку С/С++ на основе программирования учебных геодезических задач. Сборник статей по итогам международной научно-технической конференции, посвященной 230-летию основания МИИГАиК, выпуск 2, ч. 1. – М.: МИИГАиК. – 2009. – С. 199–202.

4. Заблоцкий В.Р., Васякин С.А. Применение программы «Калькулятор» в решении учебных геодезических задач. // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2004. – № 5. – С. 10–34.

5. Заблоцкий В.Р. Программирование на языке С++ для картографов и геодезистов. Учебная программа «Буссоль» с множественным наследованием. // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2016. – № 1. – С. 105–107.

6. Заблоцкий В.Р. Программирование на языке С++ для картографов и геодезистов. Учебная программа со структурой «Топографическая карта». // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2016. – № 3. – С. 105–107.

7. Заблоцкий В.Р. С++ для студентов картографов и геодезистов: учебная объектно-ориентированная программа «Перегрузка функции». // Международный журнал экспериментального образования. – 2016. – № 10–1. – С. 20–22.

8. Заблоцкий В.Р., Зеленков В.В. Учебная компьютерная программа «ТЕОДОЛИТ». Часть 1. Вычисление горизонтальных углов. // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2009. – № 4. – С. 90–100.

9. Заблоцкий В.Р., Фам Суан Хоан. Программирование учебных геодезических задач в среде BORLAND C++ BUILDER 6 (консольные приложения). // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2008. – № 4. – С.81-89.

10. Журкин И.Г., Заблоцкий В.Р., Степанов С.А. Компьютерное тестирование студентов первого курса по дисциплине «Информатика и программно-алгоритмические языки». // Известия высших учебных заведений. Геодезия и аэрофотосъемка. – 2006. – № 4. – С. 167–185.

Обсуждается учебная программа по программированию на С++ для студентов картографов и геодезистов. Опыт обучения студентов МИИГАиК программированию на С/С++ рассматривается в [1–4]. Нашей целью является разработка набора типовых учебных задач геодезического содержания [5–10], которые могут использоваться преподавателями и студентами, обучающимися по специальностям картографии и геодезии в качестве домашних заданий и при выполнении учебного практикума. Задача данной работы заключалась в разработке программы, иллюстрирующей использование пользовательских функций, на примере прямой геодезической угловой засечки.

Прямая угловая засечка позволяет определить координаты некоторой точки на основе двух исходных пунктов с известными координатами. Решение прямой угловой засечки находится по формулам котангенсов измеренных углов (формулы Юнга). Рассмотрим содержательную постановку задачи. Пусть известны координаты исходных пунктов А (XA, YA) и В (XB, YB ) между которыми имеется видимость. Требуется определить координаты пункта P (XP, YP). Измерены и известны также два горизонтальных угла: угол a между направлением на исходный пункт B и направлением на пункт P и угол b между направлением на исходный пункт A и направлением на пункт P. Для вычислений координат определяемого пункта P пользуются формулами котангенсов:

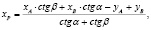
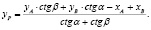
Разработанная программа решает поставленную задачу определения неизвестных координат, используя пользовательские функции, вычисления котангенса угла и преобразования угла из градусной меры в радианную. Как известно функции являются основным строительным элементом программ, написанных на основе структурного программирования. Несмотря та то, что язык С++ ориентирован на объектно-ориентированное программирование, функции продолжают играть в нем важное значение. Назначение функций заключается в обработке данных, кроме того функции разбивают большую программу на небольшие легко читаемые части кода. Поскольку функции содержат меньше строк кода, чем одна большая программа, их проще понять и удобнее модифицировать. Другое важное преимущество функций заключается в том, что функцию, созданную для одной программы, можно использовать без изменений и в другой программе. Таким образом, повторное использование функции, уменьшает трудозатраты при разработке новых программ. В нашем случае, функция convertingDegreesToRadian уже использовалась ранее в учебной программе ПЕРЕГРУЗКА ФУНКЦИИ [5]. В библиотеке стандартных функций компилятора С++ Borland отсутствует функция котангенса, имеется лишь функция тангенса. Поэтому в программе используется пользовательская функция для вычисления значения ctga, на основе тригонометрической формулы ctga = 1/tga. Другая пользовательская функция предназначена для преобразования значения угла из градусной меры в радианную меру с помощью формулы rad = a•?/180.

Рассмотрим код программы. Программа состоит из трех функций. Главная функция main представлена в строках 10-37. Функция вычисления котангенса угла ctg в строках 06-09. Функция преобразования угла из угловой меры в радианную convertingDegreesToRadian в строках 38-43. В главной функции определены переменные xA, yA, xB, yB, xP, yP типа double для хранения плановых координат известных и определяемого пункта и переменные degrees, minutes, seconds типа double для хранения горизонтальных углов при исходном направлении. Тип double переменных degrees, minutes, seconds позволяет вводить значение угла в различном формате. Например, в виде 59 °44’58» – отдельно в градусах, минутах и секундах, либо в виде 59 °44,9666’ – в градусах и минутах с дробной частью, либо только в градусах с дробной частью – 59,74944 °. В последних двух случаях пользователь вводит 0», либо 0’ и 0». В функции main вводятся все необходимые для расчета данные. Получив данные по первому исходному пункту, main вызывает функцию convertingDegreesToRadian и передает ей в качестве аргумента значение угла раздельно в градусах, минутах и секундах. Далее в строке 40 значение угла преобразуется в градусную меру, в виде целой и дробной частей градуса, а затем в строке 41 значение угла преобразуется в радианную меру. Здесь используется именованная константа M_PI, такой константой обозначается число «пи» в среде Borland C++. Преобразование угла в радианную меру выполняется потому, что в тригонометрических функциях библиотеки используются значения углов в радианах. Затем в строках 22–25 вводятся данные для второго исходного пункта. Получив необходимые данные по второму пункту, главная функция еще раз вызывает функцию convertingDegreesToRadian. В результате вычисляется координата X искомого пункта – xP (строка 30) и координата Y искомого пункта – yP (строка 31).

Данная программа иллюстрирует понятие пользовательской функции и прототипа. Прототип функции convertingDegreesToRadian представлен в строке 05. Назначение прототипа заключается в следующем. Компилятор С++ в ходе преобразования программы с языка С++ в двоичный код проверяет корректность кода и поэтому должен знать как тип возвращаемого функцией значения, так и количество и тип параметров, используемых функцией. Чтобы компилятор C++ знал особенности каждой функции до ее вызова, необходимо поместить прототипы функций в начало программы. Тогда прочитав часть кода с прототипами, компилятор получит все необходимую информацию и сможет выполнить проверку кода. Таким образом, компилятор C++ использует прототип функции convertingDegreesToRadian, чтобы убедиться в том, что тип возвращаемого функцией значения соответствует объявленному ранее, т.е double и что в качестве параметра в функцию передаются три параметра типа double. Однако прототип функции вовсе не является обязательной частью программы. Если написать программу так, чтобы код пользовательской функции находился ранее ее вызова, то в таком случае прототип оказывается излишним и его можно не использовать. В нашей программе прототип функции необходим для функции convertingDegreesToRadian, поскольку определение функции задано в строках 38–43, а вызовы этой функции выполняются в строках 20 и 27, т.е. ранее ее определения. С другой стороны определение функции котангенса ctg предшествует вызовам этой функции в программе. Поэтому компилятор C++ не нуждается в прототипе для функции ctg.

Выводы. Разработана учебная программа на языке С++ для студентов, обучающихся в геодезическом вузе. Программа демонстрирует использование функций и прототипов в задаче вычисления неизвестных плановых координат пункта по двум пунктам с известными координатами. Данная программа подчеркивает особенности структурного программирования на примере прямой геодезической угловой засечки.

Библиографическая ссылка