Основы русской инженерной школы закладывались еще в 19 столетии в виде сочетания основательной фундаментальной подготовки и широкого практического обучения. Национальная традиция обеспечения высокого уровня подготовки специалистов сохраняется в технических вузах России и в настоящее время. Более того, сейчас такая традиция становится особо актуальной. Одной из основных проблем управления подготовкой специалистов в вузах становится прогнозируемое снижение количества и качества подготовки выпускников общеобразовательных школ и уже проявляющиеся в связи с этим трудности комплектования контингента учреждений высшего профессионального образования. Наряду с этим возникает проблема адаптации студентов младших курсов к обучению в высшем учебном заведении, преодоления ими, так называемого барьера «школа – вуз» [3].
Государство и общество начинает предъявлять профессиональные требования к молодым людям все в более раннем возрасте. Это значит, что молодой человек, предполагающий добиться определенного социального статуса, должен уже в 14-16 лет определяться в профессиональном выборе. В этих обстоятельствах одной из главных задач высшей школы, заинтересованной в подготовке высококвалифицированных специалистов, становится выявление, обучение, привлечение, поощрение и поддержка научно-ориентированной, склонной к занятиям наукой и к исследовательской работе молодежи [5].
МГТУ им. Н.Э. Баумана в своей деятельности уделяет большое внимание профориентационной работе среди обучающихся средних образовательных учреждений. Для этого в Университете организуется и проводится в целях повышения заинтересованности молодежи в получении инженерного образования комплекс мероприятий, в том числе научно-образовательных [7].
Научно-образовательные мероприятия – олимпиады
Научно-образовательные мероприятия характеризуются функцией ориентации на углубленное изучение отдельных предметов, усвоение, расширение, углубление знаний в той или иной предметной области, в смежных областях знаний, адаптацией в сфере профессиональной деятельности и оптимальной самореализации для дальнейшего образования. К ним относятся интеллектуальные конкурсы, соревнования и состязания, предметные и профильные олимпиады. Данные мероприятия выступают основой воздействия не только на восприятие, память и внимание, а, прежде всего, на творческое, продуктивное мышление обучающихся. Научно-образовательная деятельность обеспечивает оптимальное сочетание самостоятельной поисковой деятельности с усвоением готовых выводов науки, формирует познавательную самостоятельность обучающихся, развитие их логического, рационального, критического и творческого мышления, способствует развитию интеллекта учащегося, его эмоциональной сферы и формированию на этой основе мировоззрения [6].
Много раз меня спрашивали и спрашивают можно ли научить решать задачи. Однозначно – можно, поскольку все мы, по большому счету, устроены одинаково и во всех нас заложено это умение. Надо только захотеть его развить в себе. Осознавая спорность моего утверждения и сложность поставленной задачи, поступим следующим образом. Я буду показывать вам разные задачи, и рассказывать о возможных методах решений, а вы, исходя из своего опыта и отталкиваясь от моих предложений, выберите свое решение. Надеюсь, вам будет из чего выбрать, поскольку методов много, а примеров их применения еще больше. Некоторые из них на первый взгляд покажутся парадоксальными [1]. Не удивляйтесь этому, поскольку одна из задач, которая неизбежно встанет перед вами – снять с вас накопленные за годы вашей жизни «зашоренность» восприятия физики. Потрясающая интересная сама по себе задача. И освоение законов кинематики как одного из начальных разделов физики – один из лучших способов ее решения.
Примеры задач и методов решений
Начнем с равномерного и прямолинейного движения.
Задача 1. Предположим, что пловцу поставлена задача переплыть реку с минимальным сносом относительно точки старта. Скорость реки – U, скорость пловца в стоячей воде – V (рис. 1). Предположим, что скорость реки по модулю больше скорости пловца, т.е. снос пловца всегда будет, как бы он не плыл. В реке пловец будет иметь скорость относительно берега VПЛ, которая определяется как сумма собственной скорости пловца и скорости реки: VПЛ = V + U. Вектор U нам известен, а у вектора V нам известен только модуль. Направление мы не знаем, его и надо найти.
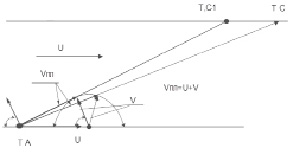
Рис. 1
Представим скорость пловца в реке иначе, поменяв местами вектора U и V (от перемены мест слагаемых сумма не изменяется): VПЛ = U + V. Кажется, что ничего не изменилось. Но на самом деле мы практически решили задачу. На рис. 1 точка А – точка старта. Отложим вектор U и к его концу добавим вектор V, возможные направления которого лежат внутри области ограниченной полуокружностью с радиусом V. Если пловец плывет под некоторым углом к берегу, то сумма скоростей определена вектором АВ, а снос будет определятся координатой точки С. Уменьшить снос можно лишь изменив угол направления движения пловца так, чтобы вектор VПЛ стал касательным к полуокружности с радиусом равным V. Отсюда сразу решение: cos α = V/U. Точка С1 определяет координату минимального сноса ( всегда по модулю ≤ 1 и это было заложено в условие задачи V < U).
Относительность движения в кинематике
Метод, использующий относительность движения, достаточно распространен при решении задач. Суть его в следующем: при выборе системы отсчета вы связываете систему координат с каким-то телом, выбор которого произволен, но чаще всего выбирают неподвижное тело. Если выбранное тело движется, то его можно сделать неподвижным, сообщив другим телам, рассматриваемым в данной задаче, относительную скорость V21 = V1 – V2 (см. рис. 2). На рис. 2 показаны два тела О1 и О2, которые двигаются относительно земли со скоростями V1 и V2, т.е. земля является той системой отсчета, относительно которой заданы параметры движения. Но можно выбрать за базовую систему отсчета систему, связанную с телом О2, которая двигается со скоростью V2. Теперь мы можем ее мысленно остановить, но при этом другим телам необходимо придать относительную скорость V21 – скорость первого тела относительно мысленно покоящегося второго тела: V21 = V1 – V2, или, если складывать скорости: V21 = V1 + (–V2). Не забудем и про землю. Теперь относительно выбранной системы отсчета она должна иметь скорость V23 = О – V2 = – V2.
Рассмотрим эффективность этого метода на примерах.
Задача 2. Тело движется со скоростью U и упруго ударяется со стенкой, которая в свою очередь движется навстречу со скоростью V (рис. 3). Определить скорость тела после удара. Масса стенки значительно больше массы тела.
Решение. Так как мы имеем дело с векторами, обратимся к рис. 3. Скорости заданы в системе отсчета, связанные с землей. Возьмем новую систему отсчета, связанную со стенкой, т.е. остановим стенку. Тогда телу необходимо сообщить относительную скорость VСТ = VT – VC = U – (–V) = U + V.
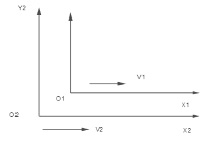
Рис. 2
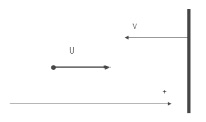
Рис. 3
После упругого удара о неподвижную стенку тело будет иметь такую же по модулю, но в обратном направлении скорость относительно стены – (U + V) = VТ – VC = VТ – (VC).
В этом выражении в правой части скорость относительно земли. Неизвестная величина VТ = –(U + 2V).
Задача 3. Человек двигаясь по полю со скоростью Vч заметил автобус, который движется по шоссе со скоростью Vа. Координаты человека и автобуса определены. Найти возможные направления движения человека, чтобы выйти к шоссе раньше автобуса.
Решение. Сделаем рис. 4.
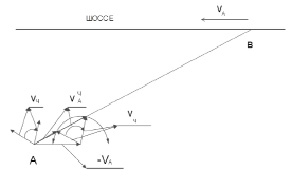
Рис. 4
Давайте упростим задачу – остановим автобус. Тогда скорость Vач = Vч – VА должна быть направлена вдоль линии АВ. Перепишем последнее равенство как сумму Vач = – VА + VЧ. Эта скорость имеет направление АВ. Из точки А откладываем вектор (– VА) и суммируем его со скоростью человека, направление которого неизвестно, но их сумма имеет направление АВ. Из рис. 4 видно, что возможные направления движения человека определены углом α. Движение человека внутри этого угла обеспечит решение поставленной задачи.
Можно продолжить примеры использования метода относительного движения, но ничего нового они не добавят к вышеизложенному.
В последнее время на олимпиадах разного уровня, появляются задачи, использующие в своем решении методы исследования функций на экстремум, с этапом дифференцирования [4]. Если функции простые, то взятие производной не вызывает затруднений, но бывают и другие случаи. Я предложу вам способ решения подобных задач без дифференцирования [1].
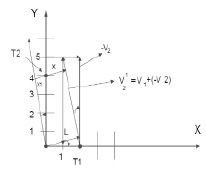
Рис. 5
Задача 4. Точки 1 и 2 двигаются равномерно по осям X и Y. В момент времени Т = 0 координата точки 1 – X0 = 2 м, а координата точки 2 – Y0 = 4 м. Первая точка движется со скоростью V1 = 1 м/с, а вторая со скоростью V2 = 5 м/с. Найти наименьшее расстояние между точками.
Решение. Сделаем рис. 5.
Попробуем остановить точку 2. Точка 1 относительно теперь уже покоящейся точки 2 будет иметь скорость V21, направление которой указано на рис. 5. Минимальное расстояние между ними равно величине X. Из очевидных построений имеем ctg α = 5, а искомое X = L – X1 = 2cos α – 4sin α = 1,2 м.
Не ортогональные системы координат в задачах равномерного движения
Метод восстановления скорости по ее проекциям довольно нагляден и прост. Если система координат выбрана ортогональной, то значение скорости по ее проекциям определяется просто (см. рис. 6).
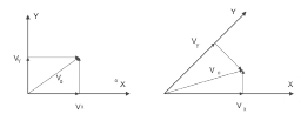
Рис. 6
А если система координат не ортогональная? Процедура восстановления скорости V0 остается прежней. А теперь как это использовать при решении.
Задача 5. Два трактора тащат бревно. В некоторый момент времени скорости тракторов равны V1 и V2, как показано на рис. 7. Определить скорость бревна.
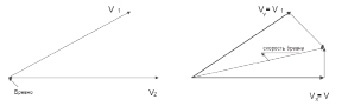
Рис. 7
Решение. Большинство, кому предлагается эта задача, пытались сложить скорости по правилу параллелограмма. Легко показать, что это ошибочный путь решения. У тела в любой момент времени может быть только одна скорость (если оно движется). В данном случае у тела скорости V1 и V2 являются проекциями реальной скорости V0 на оси X и Y. Применяя вышеописанный метод, легко восстановить скорость бревна по ее проекциям.
Следующая задача аналогична только что рассмотренным, но вызывает затруднение.
Задача 6. Лодку вытягивают из воды через блок, установленный на высоком берегу. Скорость веревки Vв. Определить скорость лодки в момент, когда угол между канатом и лодкой равен ? (см. рис. 8).
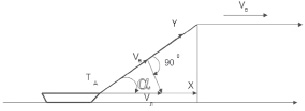
Рис. 8
Решение. Точка А принадлежит как канату, так и лодке. Лодка очевидно перемещается по оси X со скоростью Vл, а значит и точка А вдоль оси X имеет ту же скорость. Вдоль оси Y эта скорость имеет проекцию Vв, так как точка А принадлежит также и канату. Тогда Vл = Vв / cos α; именно разделить, а не умножить. Скорость лодки по мере приближения к берегу будет увеличиваться. Опять косоугольная система координат. Но в этом случае, одна из проекций Vx совпадает с искомой величиной Vл.
Применение законов геометрической оптики в задачах равномерного движения
Довольно часто в задачах на равномерное движение используются законы, которые на первый взгляд, не имеют отношения к кинематике равномерного движения [1, 2]. Попробуем более внимательно с этим разобраться. Например, дано условие: ребенок бежит вдоль длинной стенки со скоростью Vр и бросает мяч в стенку со скоростью Vм так, что при последующем движении вдоль стены он ловит отскочивший абсолютно упруго от стенки мяч. Расстояние до стенки L (см. рис. 9).
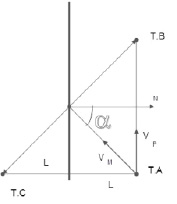
Рис. 9
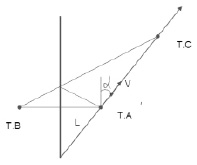
Рис. 10
Точка В – точка встречи ребенка и мяча. При решении обращаю внимание на слова «абсолютно упруго». Это значит, что угол падения мяча равен углу отражения. Используя этот факт, мяч можно бросить (конечно условно) из точки С, являющейся изображением точки А. Стена в этом случае будет играть роль плоского зеркала. А что это дает? Мы получили прямоугольный треугольник со сторонами СА = 2L, СВ = VмT, АВ = VрT, которые связаны между собой теоремой Пифагора: (Vм T)2 = 4L2 + (VрT)2. Откуда без труда находится неизвестное время T. Зная время, можно выразить любой угол 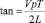 .
.
Рассмотренный метод поможет нам в решение другой довольно сложной олимпиадной задаче.
Задача 7. Автомобиль удаляется со скоростью V от длинной стены, двигаясь под углом –α к ней. В момент, когда расстояние до стены равно L, водитель подает короткий звуковой сигнал. Какое расстояние пройдет автомобиль до момента, когда водитель услышит эхо. Скорость звука – С.
Решение. Сделаем рис. 10. Используя метод плоского зеркала, пошлем сигнал из точки В. И далее применим теорему косинусов: C2T2 = V2T2 + 4L2 – 2cos(90 + α) 2L VT, откуда не без труда, но находим Т. Ну а искомое расстояние получим простым произведением V на T.
Законы отражения не единственные из законов геометрической оптики, используемые в разделе кинематика равномерного движения. Законы преломления света также находят свое применение. Например, принцип Ферма: если свет переходит из одной среды в другую, то он распространяется из точки А в точку В за минимальное время. Второй закон преломления позволяет найти соотношение между углами sin α/sin α = V1/V2. Попробуем это применить к следующей задаче.
Задача 8. Автомобиль, двигаясь из точки А, должен попасть в точку В, находящуюся от шоссе в поле на расстоянии L за минимальное время. В какой точке D, находящейся на шоссе, он должен свернуть на поле (см. рис. 11)? Дано AС = L, скорости: V1 и V2, и расстояние ВС.
Решение. Классическое решение подразумевает исследование функции времени на экстремум, т.е. задают значение длины траектории на шоссе и в поле АD = X, DC = L – X. ВС определяют по теореме Пифагора, и далее определяют время движения вдоль этой траектории. Исследуют полученное выражение на экстремум и находят значение X. Это решение имеет право на жизнь при условии умения брать производные. Но, применяя принцип Ферма, эта задача решается намного проще .Если бы свет распространялся из точки А в точку В, то это была бы траектория минимального времени sin 90/sin α = V1/V2, откуда sin α = V2/V1. Дальнейшее определение координаты точки D не вызовет затруднений.
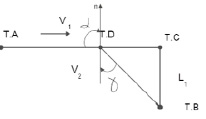
Рис. 11
Это далеко не единственная задача, где возможно применение принципа Ферма.
Заключение
Предложенные примеры задач по физике – это далеко не полный спектр возможных решений даже для задач по кинематике равномерного движения. Однако, этот далеко не полный комплекс базовых задач дает представление о том, что проведения олимпиад для школьников – это не заучивание определенных формул и не «натаскивание» на решение однотипных задач, а творческий процесс, характеризуемый функцией ориентации на углубленное изучение отдельных предметов, усвоение, расширение, углубление знаний в той или иной предметной области, в смежных областях знаний, адаптацией в сфере профессиональной деятельности и оптимальной самореализации обучающегося для дальнейшего образования.
Библиографическая ссылка
Кузин Е.И. БАЗОВЫЙ КОМПЛЕКС ЗАДАЧ И МЕТОДОВ РЕШЕНИЙ ПРИ ПОДГОТОВКЕ К ОЛИМПИАДАМ ПО ФИЗИКЕ (ЧАСТЬ 1. КИНЕМАТИКА РАВНОМЕРНОГО ДВИЖЕНИЯ) // Международный журнал экспериментального образования. – 2016. – № 9-2. – С. 189-195;URL: https://expeducation.ru/ru/article/view?id=10478 (дата обращения: 20.04.2024).

