Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Анисова Т.Л. 1 Чуев В.Ю. 1

---

1 Московский государственный технический университет им. Н.Э. Баумана

Решение иррациональных уравнений – одна из важных и сложных тем курса алгебры средней школы. Задачи по этой теме традиционно входят в единый государственный экзамен по математике. Однако опыт показывает, что учащиеся не всегда в достаточной мере владеют навыками решения иррациональных уравнений, часто допускают ошибки. Это связано с неправильным выбором метода решения того или иного уравнения. В статье показана необходимость изучения различных методов решения иррациональных уравнений. Первый метод заключается в сведении этих уравнений к равносильной системе уравнений и неравенств. При использовании второго метода обе части уравнения возводятся в квадрат, а затем проводится обязательная проверка полученных решений и отбрасывание посторонних корней. Третий метод решения требует введения вспомогательной неизвестной. Работа содержит примеры на применение различных методов и их комбинаций. Показано, что правильный выбор метода решения иррационального уравнения может значительно сократить трудоемкость процесса его решения. Также в работе содержится анализ изложения темы «Решение иррациональных уравнений» в школьных учебниках по алгебре и началам анализа различных авторов.

Статья в формате PDF

0 KB

единый государственный экзамен (ЕГЭ)

иррациональные уравнения

математика в школе

1. Кочагин В.В., Кочагина М.Н. ЕГЭ 2017. Математика: тематические тренировочные задания. – М.: ЭКСМО, 2016. – 208 с.

2. Рязановский А.Р., Мирошин В.В. ЕГЭ 2017. Математика. Решение задач. Сдаем без проблем! – М.: ЭКСМО, 2016. – 498 с.

3. Алимов Ш.А. Алгебра и начала анализа: учебник для 10–11 класса средней школы. – М.: Просвещение, 2016. – 254 с.

4. Колмогоров А.Н. Алгебра и начала анализа: учебник для 10–11 класса средней школы. – М.: Просвещение, 2008. – 384 с.

5. Виленкин Н.Я. Алгебра и математический анализ для 11 класса: учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 2014. – 288 с.

6. Башмаков М.И. Алгебра и начала анализа: учебник для 10–11 класса средней школы. – М.: Просвещение, 1992. – 351 с.

7. Мордкович А.Г., Семенов П.В. Алгебра и начала анализа. 11 класс В 2-х частях. Ч. 1. Учебник (профильный уровень). – М.: Мнемозина, 2012. – 287 с.

8. Мордкович А.Г., Семенов П.В. Алгебра и начала анализа. 11 класс (профильный уровень): методическое пособие для учителя. – М.: Мнемозина, 2010. – 191 с.

9. Мордкович А.Г. Алгебра и начала анализа. 10–11 класс: В двух частях. Ч.2: задачник для общеобразовательных учреждений. – М.: Мнемозина, 2016. – 315 с.

10. Галицкий М.Л. Сборник задач по алгебре для 8–9 классов: учебное пособие для учащихся школ и классов с углубленным изучением математики / М.Л. Галицкий. – М.: Просвещение, 2012. – 271 с.

Одной из важных задач при изучении математики в средней школе является овладение учащимися методами решения иррациональных уравнений. Иррациональные уравнения являются неотъемлемой частью школьного курса алгебры и содержатся в заданиях ЕГЭ по математике [1, 2].

Трудности при изучении данной темы связаны с тем, что зачастую отсутствует четкий алгоритм решения иррациональных уравнений. Кроме того, при решении уравнений этого типа выполняются преобразования, приводящие к уравнениям, не равносильным данным, вследствие чего возникают ошибки, которые обычно связаны с потерей корней или приобретением посторонних корней в процессе решения.

Проведенный анализ школьных учебников по алгебре и началам анализа позволяет сделать следующие выводы:

– В учебнике Ш.А. Алимова [3] материал по методам решения иррациональных уравнений отсутствует.

– В учебниках А.Н. Колмогорова [4] и Н.Я. Виленкина [5] теоретического материала по решению иррациональных уравнений достаточно. В большом объеме теория рассмотрена в учебниках М.И. Башмакова [6] и А.Г. Мордковича [7, 8].

– В каждом учебнике рассмотрены основные способы решения: сведение иррациональных уравнений к системе уравнений и неравенств с помощью равносильных переходов, а также возведение обеих частей уравнения в квадрат и последующая подстановка полученных корней в исходное уравнение для проверки.

– Наибольший большой объем упражнений для решения иррациональных уравнений содержится в задачниках А.Г. Мордковича [9] и М.Л. Галицкого [10].

Существуют два метода решения иррациональных уравнений вида

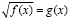и

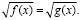
Первый метод заключается в сведении этих уравнений к равносильной системе уравнений и неравенств.

Уравнение 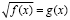сводится к системе

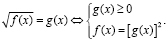
Неравенство f(x) ≥ 0 решать не нужно, так как оно является следствием уравнения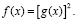

Уравнение вида 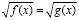сводится к системе

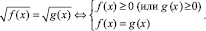
Поскольку неотрицательное число не может равняться отрицательному, достаточно решить одно из двух неравенств: f(x) ≥ 0 или g(x) ≥ 0.

При использовании второго метода обе части уравнения возводятся в квадрат, а затем проводится обязательная проверка полученных решений и отбрасывание посторонних корней.

Однако нередко учителя излагают только один метод решения иррациональных уравнений, что приводит к достаточно серьезным осложнениям при решении учащимися некоторых задач. Необходимость изучения обоих методов решения иррациональных уравнений проиллюстрируем на следующих примерах.

Пример 1. Решить уравнение:

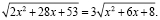
Используем первый метод. Так как корни уравнения 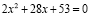являются иррациональными числами 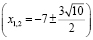, для решения уравнения запишем следующую систему:

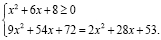
Решим уравнение 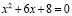. Его корнями являются x1 = –4 и x2 = –2.

Решением неравенства уравнение 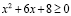является объединение интервалов .

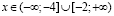Преобразуем уравнение системы. Получаем 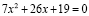. Найдем его корни.

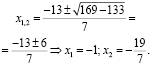
При этом корень 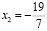является посторонним, так как он не удовлетворяет неравенству системы.

Таким образом, окончательный ответ: x = –1.

Отметим, что при использовании второго метода проверка корня 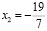является достаточно трудоемким процессом, при выполнении которого учащиеся довольно часто делают вычислительные ошибки.

Пример 2. Решить уравнение:

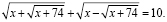
Используем второй метод. Возведя обе части уравнения в квадрат, получаем

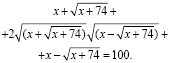
После преобразований приходим к уравнению

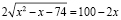
или

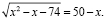
Еще раз возводим обе части уравнения в квадрат:

.

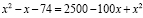Окончательно получаем

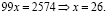
Проверим полученное решение. Подставим x = 26 в исходное уравнение:

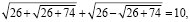
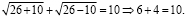
Получаем тождество, т.е. x = 26 является корнем этого уравнения.

При использовании первого метода получаем систему неравенств

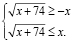
Выражение 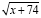не может быть отрицательным. Из второго неравенства следует, что x ≥ 0, поэтому – x ≤ 0. Это означает, что первое неравенство системы оказывается лишним.

Неравенство 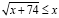эквивалентно системе

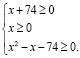
Решим уравнение 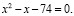Его корнями являются

.

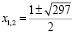Получаем

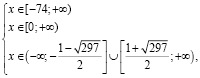
т.е. область допустимых значений (ОДЗ) этого уравнения имеет вид

. (*)

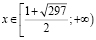В дальнейшем требуется провести те же алгебраические преобразования, что и при применении второго метода, и убедиться, что полученное решение x = 26 принадлежит полуинтервалу (*).

Очевидно, что применение этого метода оказывается в данном случае достаточно громоздким, т.е. при решении данного уравнения целесообразно использовать второй метод.

При решении отдельных иррациональных уравнений целесообразно комбинировать оба вышеизложенных метода. Проиллюстрируем это на следующем примере.

Пример 3. Решить уравнение:

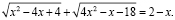
Так как в левой части уравнения находится сумма двух неотрицательных чисел, получаем 2 – x ≥ 0 или x ≤ 2.

Преобразуем левую часть уравнения:

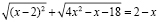
или

.

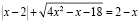Так как x ≤ 2, то 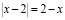, поэтому

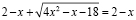
или

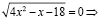
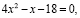
поэтому неравенство 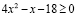решать не нужно.

Решая полученное уравнение, находим его корни x1 = –2; 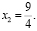Так как x ≤ 2, то корень 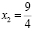оказывается посторонним. Проводить проверку полученного решения в данном случае не требуется. Получаем окончательный ответ: x = –2.

Решение некоторых иррациональных уравнений практически сводится к нахождению области их допустимых значений (ОДЗ), в чем можно убедиться на следующем примере.

Пример 4. Решить уравнение:

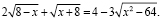
Запишем ОДЗ:

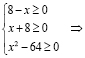
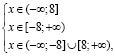
т.е. ОДЗ этого уравнения состоит только из двух чисел: x1 = –8; x2 = 8. Подставим эти числа в уравнение.

При x1 = –8 получаем

,

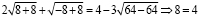т.е. x1 = –8 корнем уравнения не является.

При x2 = 8

,

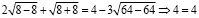т.е. получим тождество.

Таким образом, данное уравнение имеет одно решение x = 8.

Заметим, что использование первого метода практически сразу привело к нахождению корня этого уравнения.

Попробуем для решения этого уравнения использовать второй метод. Возведем обе части уравнения в квадрат:

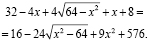
После преобразований получаем

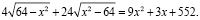
Для избавления от радикалов необходимо возвести обе части уравнения в квадрат. Это приведет к необходимости решения уравнения четвертой степени, что не входит в школьную программу изучения математики. Однако использовать первый метод можно и на этом этапе, т.к. решение системы неравенств

⇒

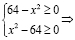
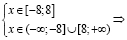
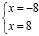
приводит к тому, что ОДЗ этого уравнения состоит только из двух чисел x1 = 8 и x2 = –8.

При решении уравнений вида

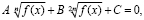
где f(x) – линейная функция или квадратный трехчлен, используется метод введения новой неизвестной, 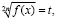t₀ ≥ 0, что приводит к квадратному уравнению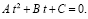

Решаем это уравнение, отбрасываем посторонние корни (t < 0) и приходим к уравнению f(x) = t₀, t₀ ≥ 0.

Решая его, получаем окончательный ответ.

В частности, для уравнения вида 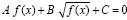получаем

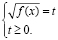
Проиллюстрируем изложенный метод на следующем примере.

Пример 5. Решить уравнение:

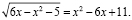
Преобразуем правую часть этого уравнения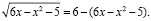

Введем новую неизвестную

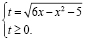
Приходим к уравнению 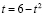или 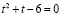. Находим его корни t1 = 2 и t2 = –3.

Второй корень t2 = –3 является посторонним, т.к. t₀ ≥ 0.

Далее получаем

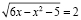
или

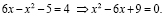
Это уравнение имеет один корень x = 3. Проверку полученного решения проводить не требуется, т.к. из равенства 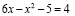следует, что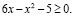

Получаем окончательный ответ x = 3.

Отметим, что использование для решения этого уравнения любого из ранее изложенных методов требует возведения обеих частей уравнения в квадрат, что приводит к необходимости решать уравнение четвертой степени.

Приведенные выше примеры наглядно подтверждают необходимость изучения всех методов решения иррациональных уравнений. К сожалению, невозможно выработать общие рекомендации по поводу того, в каких случаях какой из вышеизложенных методов следует использовать при решении предложенного иррационального уравнения. Можно дать один практический совет: если система уравнений и неравенств для нахождения ОДЗ уравнения получается очень сложной и громоздкой, следует использовать второй метод решения или комбинацию первого и второго методов.

Библиографическая ссылка