Научный журнал

Международный журнал экспериментального образования

ISSN 2618–7159

ИФ РИНЦ = 0,425

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нахман А.Д. 1 Осиленкер Б.П. 2

---

1 ФГБОУ ВПО «Тамбовский государственный технический университет»

2 НИУ «Московский государственный строительный университет»

Изучено поведение семейства операторов 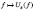, определяемых экспоненциальными методами суммирования 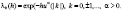При некоторых условиях на функцию 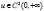установлена сходимость 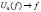(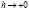) в каждой точке Лебега.

Статья в формате PDF

2943 KB

выпуклые

кусочно-выпуклые последовательности

линейные средние рядов Фурье

сходимость в точках Лебега

1. Зигмунд, А. Тригонометрические ряды. T.1 / А. Зигмунд. – М.: Мир, 1965. – 615 с.

2. Nakhman, A.D. Weigted norm inequalities for the convolution operators / A.D. Nakhman // Transactions TSTU. – 2009. – V.15, № 3. – P. 653-660.

3. Никольский, С.М. О линейных методах суммирования рядов Фурье / С.М. Никольский // Известия АН СССР, сер. матем. – 1948. – № 12. – С.259 –278.

Пусть 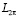– класс 2 π-периодических суммируемых на 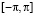функций, С2π – класс 2 π-периодических непрерывных функций, 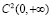– класс функций, обладающих непрерывными на 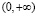вторыми производными. В настоящей работе рассматриваются экспоненциальные средние

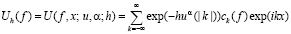(1.1)

рядов Фурье функций 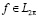. В определении (1.1)

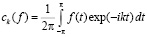, (1.2)

– коэффициенты Фурье функции f, 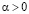– произвольный фиксированный параметр, функция 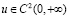принимает положительные значения,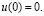

Одна из основных задач, рассматриваемых в настоящей работе – изучение поведения семейства операторов 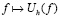при 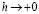. А именно, мы будем изучать сходимость (1.1) в точках Лебега, т.е. в точках х, обладающих свойством

.

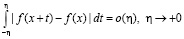Точки Лебега, как известно ([1], с. 111 ), расположены почти всюду для каждой .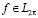

Частными случаями (1.1) являются

1) решение

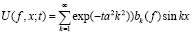
задачи теплопроводности

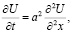
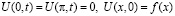
в стержне длины π с постоянным коэффициентом температуропроводности a2 (t>0 – время протекания процесса, 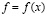– заданное распределение начальных температур, 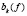– синус-коэффициенты Фурье функции f );

2) решение

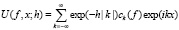(1.3)

задачи Дирихле

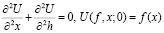
в полуплоскости (нахождение стационарного распределения температур в точках 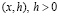с заданной на границе 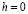температурой 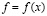). Операторы, определяемые соотношением (1.3) известны как средние Пуассона-Абеля ([1], с. 160-165) и играют значительную роль в различных вопросах анализа. Однако, не до конца изучено ([2]) даже наиболее простое и естественное обобщение

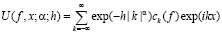(1.4)

средних (1.3) на случай любого 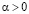. Речь идет, в частности, об (1.4) как решении обобщенной задачи Дирихле в полуплоскости

,

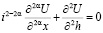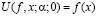, (1.5)

где дифференцирование по х есть соответствующее дробное дифференцирование, а (1.5) понимается как предельное соотношение

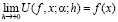(1.6)

(характер сходимости обсуждается ниже).

2. Основной результат

Теорема 2.1.

Пусть 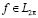и при каждом h>0

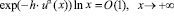. (1.7)

1) Если 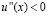при всех 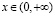и 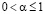, то соотношение

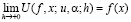(1.8)

имеет место в каждой точке Лебега функции f и равномерно по х для всякой f∈ С2p.

2) Результат (1.8) сохраняется для 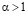, если (в дополнение к (1.7) ) существует постоянная 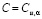, такая, что при всех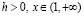

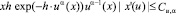, (1.9)

и функция

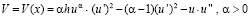(1.10)

имеет на конечное число нулей.

3. Вспомогательные утверждения. Рассмотрим бесконечную произвольную последовательность

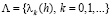, (2.1)

определяемую значениями параметра h>0, и соответствующее семейство линейных средних ряда Фурье произвольной f∈ L2π

.

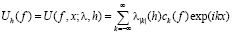Последовательность (2.1) называется выпуклой (вогнутой), если

,

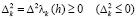где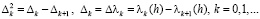

Последовательность (2.1) кусочно-выпукла, если 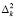меняет свой знак конечное число раз, 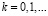Поведение линейных средних рядов Фурье, определяемых выпуклыми конечными последовательности изучались в работе С.М. Никольского [3]. В следующем утверждении (имеющем и самостоятельный интерес) некоторые результаты [3] распространяются на «полунепрерывный» случай (2.1).

Лемма 2.1. Пусть последовательность (2.1) выпукла (вогнута) и при каждом 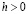ее члены удовлетворяют условиям

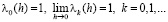(2.2)

и

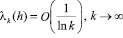. (2.3)

Тогда соотношение

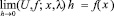(2.4)

имеет место в каждой точке Лебега функции f и равномерно по х для всякой f∈С2p.

Утверждение сохраняется, если последовательность (2.1) кусочно-выпукла, выполнено условие (2.3) и существует постоянная C (зависящая лишь от λ) такая, что при всех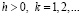

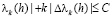|. (2.5)

Доказательство. Пусть

.

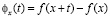Воспользовавшись интегральной формой (1.1) коэффициентов Фурье и преобразованием Абеля ([1], c.15), запишем

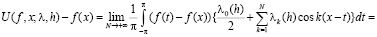
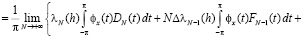
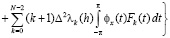, (2.6)

где

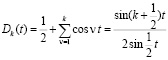и

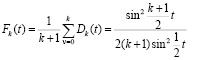
– соответственно, ядро Дирихле и ядро Фейера ([1], с.86, 148). Согласно классическим результатам ([1], с.113, 151) для любого 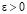в каждой точке Лебега имеют место соотношения

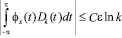и

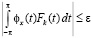
при всех значениях k, больших некоторого 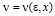; постоянная С в первом из неравенств не зависит от k. Учитывая (2.3), очевидные оценк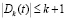и и 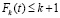и считая, что 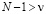в (2.5), получим теперь, что модуль выражения, записанного под знаком предела в (2.6), не превосходит суммы

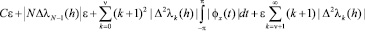. (2.7)

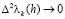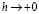Далее, согласно (2.2), при и 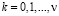. Кроме того, для выпуклой последовательности при каждом 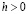имеют место соотношения ([1], с. 155-156)

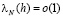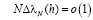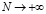, при (2.8)

и (в силу преобразования Абеля)

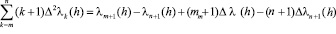; (2.9)

в (2.8) т и п – любые натуральные числа, причем m<n

В частности, согласно (2.9), (2.3) и (2.8)

,

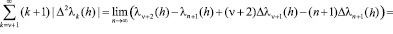
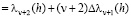и теперь из (2.6) вытекает, что

.

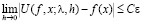Отсюда, ввиду произвольности ε, и следует выполнимость соотношения (2.4) в каждой точке Лебега.

Далее, согласно преобразованиям типа (2.6) и соотношениям (2.3), (2.8), (2.9) для нормы 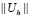каждого из операторов 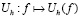, действующего из С2p в С2p справедлива оценка

,

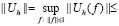
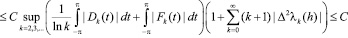где постоянная С зависит лишь от l. Следовательно, равномерная по х сходимость (2.4) имеет место в силу теоремы Банаха-Штейнгауза.

Если же последовательность L кусочно-выпукла, так что 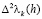сохраняет свой знак при 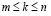для некоторых натуральных m и n, то сумма 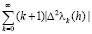равна конечному числу (числу перемен знаков последовательности 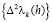) блоков-слагаемых, каждый из которых имеет вид (2.9); преобразование суммы (2.9) с 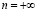предполагает использование соотношения (2.8). Остается применить к полученным слагаемым оценку (2.5) и повторить рассуждения, использованные в случае выпуклой (вогнутой) последовательности (2.1). Лемма полностью доказана.

4. Доказательство теоремы 2.1. Пусть теперь

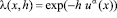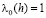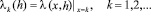, , (4.1)

В этом случае, согласно (4.1),

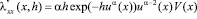, (4.2)

где 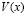определена соотношением (1.10).

Есл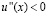и и 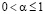, то согласно (4.2), последовательность (4.1), оказывается выпуклой, а значит, к ней применима лемма 3.1; при этом условие (2.3) выполнено в виде (1.7). Первая часть теоремы 2.1 доказана.

Для доказательства второй части заметим, прежде всего, что сформулированное условие на функцию V(x) в (1.10) обеспечивают кусочную выпуклость последовательности (4.1). Действительно, пусть, например, V(x) знакопостоянна при 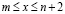(т и п – некоторые неотрицательные целые числа). Применим к 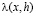, как функции от х, дважды теорему Лагранжа: первый раз на отрезке [k, k+1], так что

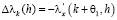, (4.3)

а второй раз на отрезке :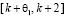

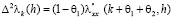, (4.4)

где 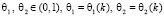. При 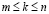будем иметь 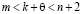, где 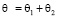а значит, вторые разности (4.4) в сумме вида (2.9) будут знакопостоянными. Поскольку число интервалов с целочисленными концами, на которых V(x) знакопостоянна, является конечным, то и 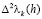имеет конечное число перемен знака. Условие же (1.9) является достаточным (см. (4.3)) для выполнимости соотношения (2.5). Этим и заканчивается доказательство теоремы 2.1.

5. Примеры.

5.1. Пусть 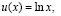так что

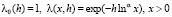. (5.1)

При этом (см. (2.3)) 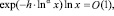если 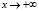, в чем можно легко убедиться, применяя правило Лопиталя n раз, где n – наименьшее натуральное число, для которого 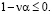Следовательно, при 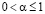для случая (5.1) выполнены условия п.1 теоремы 2.1, и, следовательно, справедливо ее утверждение. Если же 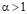, то 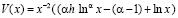и выражение в скобках возрастает с ростом х, а значит, обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех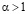

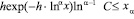
что очевидно для 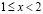и остается справедливым для 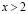, поскольку функция

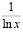
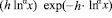
ограничена вместе с функцией вида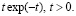

Итак, утверждения теоремы 2.1 справедливы для случая (5.1) при всех 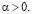В частности, (случай α=1) сумма ряда

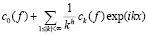
при 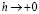стремится к значениям f(x) для почти всех х () и равномерно по х в случае f∈С2π

5.2. Пусть 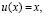так что

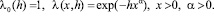(5.2)

В этом случае получаем обобщенные средние Пуассона (1.4); классические средние Пуассона соответствуют случаю 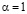и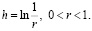

Очевидно, что 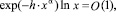если 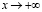, т.е. выполнено условие (1.7), а тогда при 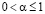для случая (5.2) справедливо утверждение теоремы 2.1. Если же 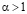, то функция 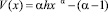обращается в ноль ровно при одном значении х. Следовательно, соответствующая последовательность (4.1) кусочно-выпукла. Остается проверить, что (см. (2.5), (1.9)) при всех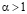

,

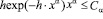что очевидно, поскольку функция 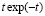ограничена при всех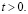

Следовательно, утверждения теоремы 2.1 справедливы для случая (5.2) при всех 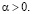В частности, получаем, что средние (1.4) служат решением обобщенной задачи Дирихле (п. 1), причем граничное условие (1.5) выполняется в виде (1.6) в каждой точке Лебега функции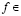 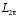и равномерно по x для всякой f∈С2p.

Близким к рассмотренному является пример полиномиально-экспоненциального метода суммирования, определяемого (см. (4.1)) функцией

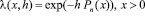, (5.3)

где 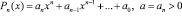– произвольный многочлен n-й степени, 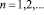Функция 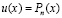принимает только положительные значения при достаточно больших х; в частности, существует постоянная C>0, такая, что 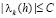при всех 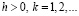В силу (5.3) 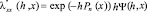, причем

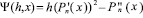. (5.4)

Многочлен (5.4) имеет степень 2n – 2, так что меняет знак не более 2n – 2 раз. Следовательно, выполнено условие кусочной выпуклости последовательности (4.1).

Проверим условия (1.9). Имеем в левой части (1.9)

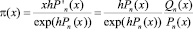. (5.5)

Здесь дробь 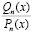, в которой 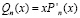, ограничена, поскольку отношение старших коэффициентов многочленов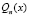 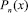равно n. Первая же дробь в (5.5) ограничена, поскольку она имеет вид 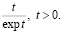Следовательно, все произведения (5.5) ограничены некоторой постоянной.

Итак, условия теоремы 2.1 выполнены для полиномиально-экспоненциальных средних, определяемых функцией (5.3), а значит и в этом случае справедливо ее утверждение.

Заметим, что даже частные случаи основного утверждения (п.2) настоящей работы, исследованные в п.5, являются новыми и представляют самостоятельный интерес.

Библиографическая ссылка